Switch Transformers 论文详解

Categories: LLM_Parallel 2025-06-24

一背景知识
二 MoE 负载不均衡的优化
三 MoE 并行策略
参考资料

一背景知识

1.1 All-to-All 通信

llm 推理部署中的 All-to-All 通信包括：Dispatch 和 Combine 阶段。

Dispatch（分发阶段）：将本地数据分片发送给其他节点（例如张量的不同维度分片）。
Combine（聚合阶段）：从所有节点收集分片并重组为完整数据。

1.2 MoE 专家并行原理

1，概述：

专家并行是在分布式学习中专门针对 MoE 模块场景的并行策略，其主要思想就是将不同专家放在不同计算节点上进行并行计算。
专家并行与之前所有的并行相比，最大的不同在于，输入数据需要通过一个动态的路由选择机制分发给相应专家，此处会涉及到一个所有节点上的数据重分配的动作（dispatch），然后在所有专家处理完成后，又需要将分散在不同节点上的数据按原来的次序整合起来（combine）。
对于专家并行，通信发生在每一个 MoE 模块之前和之后，即 dispatch 和 combine 操作，单次通信数据量较大且可能动态变化，通信较频繁。

2，核心思想：

动态专家激活：MoE 模型中，每个输入 token 仅被路由到 num_experts_per_tok个专家（如DeepSeek R1 每层激活 8/256 个专家），其他专家处于空闲状态。

3，关键挑战和优化：

负载不均衡：高频专家导致部分 GPU 过载（如负载波动达300%）。【解决办法：EPLB 优化: 存放冗余专家】
通信开销：跨节点通信（如 RDMA）延迟高。【解决办法：高度优化的通信库 DeepEP, 通信和计算重叠】

1.3 DeepSpeed MoE 并行策略

DeepSpeed MoE 支持五种不同形式的并行，并同时利用 GPU 和 CPU 内存。其灵活的设计使用户能够混合不同类型的流行并行技术，如下表所示。

简称	灵活并行配置	优势
E	专家并行	通过增加专家数量来扩展模型大小
E + D	专家 + 数据并行	通过扩展到多个数据并行组来加速训练吞吐量
E + Z	专家 + ZeRO 驱动的数据并行	分割非专家参数以支持更大的基础模型
E + D + M	专家 + 数据 + 模型并行	支持巨大的隐藏层大小，以及比 E+Z 更大的基础模型
E + D + Z	专家 + 数据 + ZeRO 驱动的数据并行	支持巨大的隐藏层大小，以及比 E+Z 更大的基础模型
E + Z-Off + M	专家 + ZeRO-Offload + 模型并行	在有限的 GPU 数量下，为大型 MoE 模型利用 GPU 和 CPU 内存

二 MoE 负载不均衡的优化

设置专家容量 (Expert Capacity)：这是这段代码最核心的概念。在 TPU 这样的硬件上，为了效率最大化，计算图（包括张量的形状）在编译时必须是静态的。你不能动态地决定一个专家今天处理 100 个 tokens，明天处理 120 个。因此，每个专家都被分配了一个固定大小的缓冲区，这就是它的“容量”。如果发送给某个专家的 tokens 数量超过了其容量，多余的 tokens 就会被丢弃 (dropped)。
负载均衡损失 (Load Balancing Loss)：由于存在 token 丢弃的风险，我们不希望路由器把所有 tokens 都发送给少数几个“热门”专家。因此，需要一个辅助的损失函数来鼓励路由器尽可能均匀地将 tokens 分配给所有专家。

load_balancing_loss

负载均衡损失优化的完整公式如上图所示。

公式4: 负载均衡损失

\[\text{loss} = \alpha \cdot N \cdot \sum_{i=1}^{N} f_i \cdot P_i\]

$f_i$：实际分配到专家 $i$ 的 token 比例（公式5）
- 计算方式：统计 batch 内被路由到专家 i 的 token 数量，除以总 token 数 T 。
- 例如：若 100 个 token 中有 30 个分配给专家 1，则 $f_1 = 0.3$。
$P_i$：路由器对专家 $i$ 分配的概率均值（公式6）
- 计算方式：对 batch 内所有 token 的路由概率 $p_i(x)$ 取平均。
- 例如：若所有 token 对专家 1 的平均概率为 0.2，则 $P_1 = 0.2$ 。
$\alpha$：超参数，控制损失权重, 文中设为 $10^{-2}$。
$N$：专家总数，用于抵消专家数量对损失值的影响。

关键设计思想

目标：最小化该损失会迫使 $f_i$ 和 $P_i$ 趋近于 $\frac{1}{N}$（即均匀分配）。
- 当完全均衡时：$f_i = P_i = \frac{1}{N}$，此时损失值为 $\alpha \cdot N \cdot \sum \frac{1}{N^2} = \alpha$与 $N$ 无关。
可微分性：仅 $P_i$ 依赖可微的路由概率，而 $f_i$ 不可微（因 argmax 是离散操作），但整体损失仍可梯度传播。

公式5：实际分配比例 $f_i$

\[f_i = \frac{1}{T} \sum_{x \in B} 1 {\text{argmax } p(x) = i}\]

($ 1{\cdot} $): 指示函数，当token $x$被分配给专家$i$时值为1，否则为0。
物理意义：直接统计各专家的真实负载比例。

公式6：路由概率比例 $P_i$

\[P_i = \frac{1}{T} \sum_{x \in B} p_i(x)\]

$p_i(x)$：token $x$ 分配给专家 $i$ 的软概率（由路由器输出）。
物理意义：量化路由器对专家 $i$ 的”偏好程度”。

为什么该损失能促进负载均衡

数学性质：当 $f_i$ 和 $P_i$ 均等于 $\frac{1}{N}$ 时，损失达到最小值 $\alpha$。
反向传播作用：
- 若某专家 $i$ 的 $f_i$ 过高（接收过多 token），损失函数会通过 $P_i$ 调整路由概率，减少对该专家的偏好。
- 反之，若 $f_i$ 过低，则增加路由概率。

举个例子，假设 $N=2$ 个专家，batch 内 $T=4$ 个token：

Token $x$	专家1概率 $p_1(x)$	专家2概率 $p_2(x)$	实际分配
$x_1$	0.7	0.3	专家1
$x_2$	0.6	0.4	专家1
$x_3$	0.4	0.6	专家2
$x_4$	0.3	0.7	专家2

计算：
- $f_1 = \frac{2}{4} = 0.5$, $f_2 = 0.5$
- $P_1 = \frac{0.7+0.6+0.4+0.3}{4} = 0.5$, $P_2 = 0.5$
- 损失值：$\alpha \cdot 2 \cdot (0.5 \cdot 0.5 + 0.5 \cdot 0.5) = \alpha$（均衡状态）

三 MoE 并行策略

llm 并行推理时：数据并行 + 模型并行（张量并行），GPU 数量 = dp_size * tp_size。

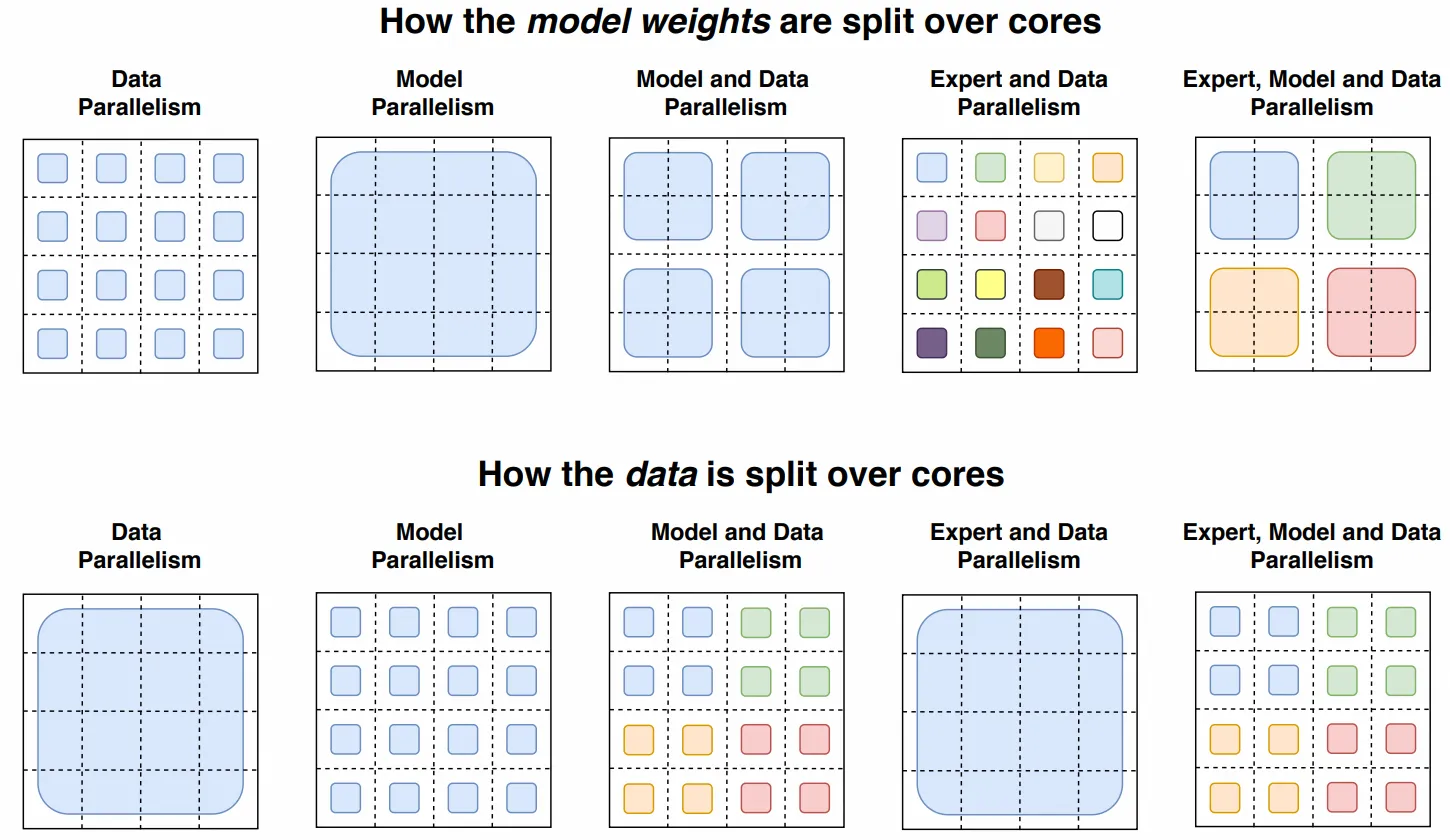
moe_parall

3.1 数据并行 + 张量并行

每个 gpu 设备负责: $\text{num_tokens} / \text{dp_size}$ 个 tokens，以及 $\text{d_model} / m$、$\text{d_ff} / m$ 的权重和中间激活。在前向传播和反向传播过程中，每个核心通过全归约操作传输大小为: $[\text{num_tokens} / \text{dp_size},\text{d_model}]$ 的张量。

3.2 数据并行 + 专家并行

首先，定义文中的变量：

n: 计算核心的数量（例如 GPU 或 TPU 核心的数量）。
B: 一个批次中 Token 的总数 (Total Batch Size)。
B/n: 每个核心处理的 Token 数量。
E: 模型中专家的总数。
C: 每个专家的容量 (Capacity)，即每个专家最多能处理的 Token 数量。
d_model: 模型的隐藏层维度（Token 的向量表示维度）。

流程分解

第一步：本地路由 (Local Routing)

Switch Transformer 的一个巧妙设计是：如果你有 n 个计算核心（如 GPU），那么你就有 n 个专家，每个核心恰好负责一个专家。

“Switch Transformers will allocate all of their cores to the data partitioning dimension n… For each token per core a router locally computes assignments to the experts.”

“Switch Transformers 会将所有计算核心分配至数据分区维度 n… 每个核心上的令牌会由本地路由器计算专家分配方案。”

初始状态：系统处于数据并行模式。有 n 个计算核心（如 GPU），就有 n 个专家，每个核心负责一个专家，处理 B/n 个 tokens。
本地计算：在每个核心上，路由器独立地为它自己负责的 B/n 个 tokens 计算出它们应该去哪个专家。
输出：路由器的计算结果是一个巨大的、稀疏的二进制矩阵，我们称之为 dispatch_tensor。对于单个核心来说，它的形状是 [B/n, E, C]。当所有 n 个核心组合起来时，就是文中的 [n, B/n, E, C]。这个矩阵标记了每个本地 token 应该去哪个专家（E 维度）的哪个容量位置（C 维度）。

第二步：本地收集 (Local Gather via `einsum`)

“This binary matrix is then used to do a gather via matrix multiplication with the input tensor… einsum(…)”

“随后通过该二进制矩阵与输入张量…的矩阵乘法来完成数据收集操作。”

操作：这是一个非常聪明的步骤。通过 einsum（本质上是矩阵乘法），dispatch_tensor 被用来从原始的 token 列表 [n, B/n, d_model] 中“抓取”和“排序” tokens。
einsum 详解:
- einsum([n, B/n, d_model], [n, B/n, E, C], dimension=[B/n])
- 输入1: [n, B/n, d_model] - 每个核心上的原始 token 数据。
- 输入2: [n, B/n, E, C] - 本地路由决策（调度矩阵）。
- 操作: 它在 B/n 这个维度上进行收缩（矩阵乘法）。可以理解为，对于每个核心，它都在说：“按照我的调度矩阵，把这 B/n 个 tokens 重新排列，放进 E 个专家的 C 个容量槽里。”
结果：einsum 的输出张量形状为 [n, E, C, d_model]。
- 含义：此时，在每个核心上，tokens 已经根据它们将要去的专家被分好组了。例如，在核心0上，有一个形状为 [E, C, d_model] 的张量，其中第一个切片 [0, C, d_model] 是所有起源于核心0并且要去专家0的 tokens，第二个切片是起源于核心0要去专家1的 tokens，依此类推。
- 关键问题：虽然 tokens 已经按专家分组，但它们仍然在错误的物理核心上。例如，要去专家5的 tokens 现在可能还分散在核心0、核心1、核心2…上。

第三步：全局交换 (Global Shuffle via `All-to-All`)

“Because each core has its own expert, we do an all-to-all communication… to now shard the E-dimension instead of the n-dimension.”

“由于每个计算核心拥有独立的专家模块，我们需执行…的全交换通信，将分片维度从 n 维度转为 E 维度。”

模式切换：这是从数据并行切换到专家并行的魔法发生的地方。我们现在假定，物理核心 $i$ 负责运行专家 $i$。
All-to-All操作：
- 发送：核心 i 会把它在上一步中收集好的、要去往专家 j 的那一包 tokens ([j, C, d_model]) 发送给核心 j。它会对所有 j 都做这个操作。
- 接收：同时，核心 i 会从所有其他核心 j 那里，接收它们发送过来的、要去往专家 i 的那一包 tokens。
最终状态：经过 All-to-All 之后，在核心 i 上，现在汇集了来自所有核心的、但目标都是专家 i 的 tokens。此时，核心 i 就可以用它负责的专家 i 的权重对这些 tokens 进行计算了。数据的分片方式从按 n（数据并行）变成了按 E（专家并行）。

实例分析

假设我们有以下配置：

n=2 (2个GPU: GPU0, GPU1)
E=2 (2个专家: E0, E1)，我们规定 GPU0 负责 E0，GPU1 负责 E1。
B=8 (总共8个tokens: t0-t7)
B/n=4 (每个GPU处理4个tokens)
C=3 (每个专家容量为3)
d_model=... (维度不影响逻辑)

1. 初始状态 (数据并行)

GPU0 持有数据：[t0, t1, t2, t3]
GPU1 持有数据：[t4, t5, t6, t7]

2. 本地路由 & 本地收集 (einsum)

GPU0 上的路由器决定：
- t0 -> E1
- t1 -> E0
- t2 -> E1
- t3 -> E0
  经过 einsum，GPU0 上的张量 [E, C, d_model] 变为：
- 发往 E0 的包：[t1, t3, <pad>] (容量3，填满2个)
- 发往 E1 的包：[t0, t2, <pad>] (容量3，填满2个)
GPU1 上的路由器决定：
- t4 -> E1
- t5 -> E1 (但 E1 容量已满，假设 t5 被丢弃)
- t6 -> E0
- t7 -> E1
  经过 einsum，GPU1 上的张量 [E, C, d_model] 变为：
- 发往 E0 的包：[t6, <pad>, <pad>]
- 发往 E1 的包：[t4, t7, <pad>] (t5 被丢弃了)

3. 全局交换 (All-to-All)

GPU0：
- 发送去往 E1 的包 [t0, t2, <pad>] 给 GPU1。
- 保留去往 E0 的包 [t1, t3, <pad>]。
- 接收来自 GPU1 的、去往 E0 的包 [t6, <pad>, <pad>]。
GPU1：
- 发送去往 E0 的包 [t6, <pad>, <pad>] 给 GPU0。
- 保留去往 E1 的包 [t4, t7, <pad>]。
- 接收来自 GPU0 的、去往 E1 的包 [t0, t2, <pad>]。

4. 最终状态 (专家并行)

GPU0 上现在的数据是 所有要去 E0 的 tokens: [t1, t3, t6]。GPU0 现在可以调用 专家E0 进行计算。
GPU1 上现在的数据是 所有要去 E1 的 tokens: [t0, t2, t4, t7] (注意，这里的数量超过了容量C，说明我的例子中 t7 也应该被丢弃，一个更真实的场景是容量会被严格遵守)。一个更正的例子是 GPU1 的包是[t4, t7, <pad>]，接收 GPU0 的包[t0, t2, <pad>]后，最终送入 E1 计算的是[t4, t7, t0]，t2被丢弃。

计算完成后，会再有一次 All-to-All 将结果发送回它们原始的 token 位置。

3.3 专家、数据、张量并行

一个 gpu 的显存是有限的，可能不足以存放下所有 experts 的权重，因此需要增加 m（张量并行）。但由于核心（GPU）数量 N 和 N=n×m 是固定的，我们必须减少 n ，这迫使采用更小的批处理规模（以保持每个核心处理的令牌数恒定）。当结合模型并行与专家并行时，我们将面临两种通信开销：一是将令牌路由至对应专家的全对全通信，二是模型并行内部的全局规约通信。当同时采用这三种方法时，平衡 FLOPS、通信开销与单核内存变得极为复杂，最佳映射方案需通过实验确定。

参考资料

你觉得有收获吗？❤️