MLA 结构代码实现及优化
Categories: Transformer
1. MLA 计算拆解
MLA 结构的可视化图如下所示:
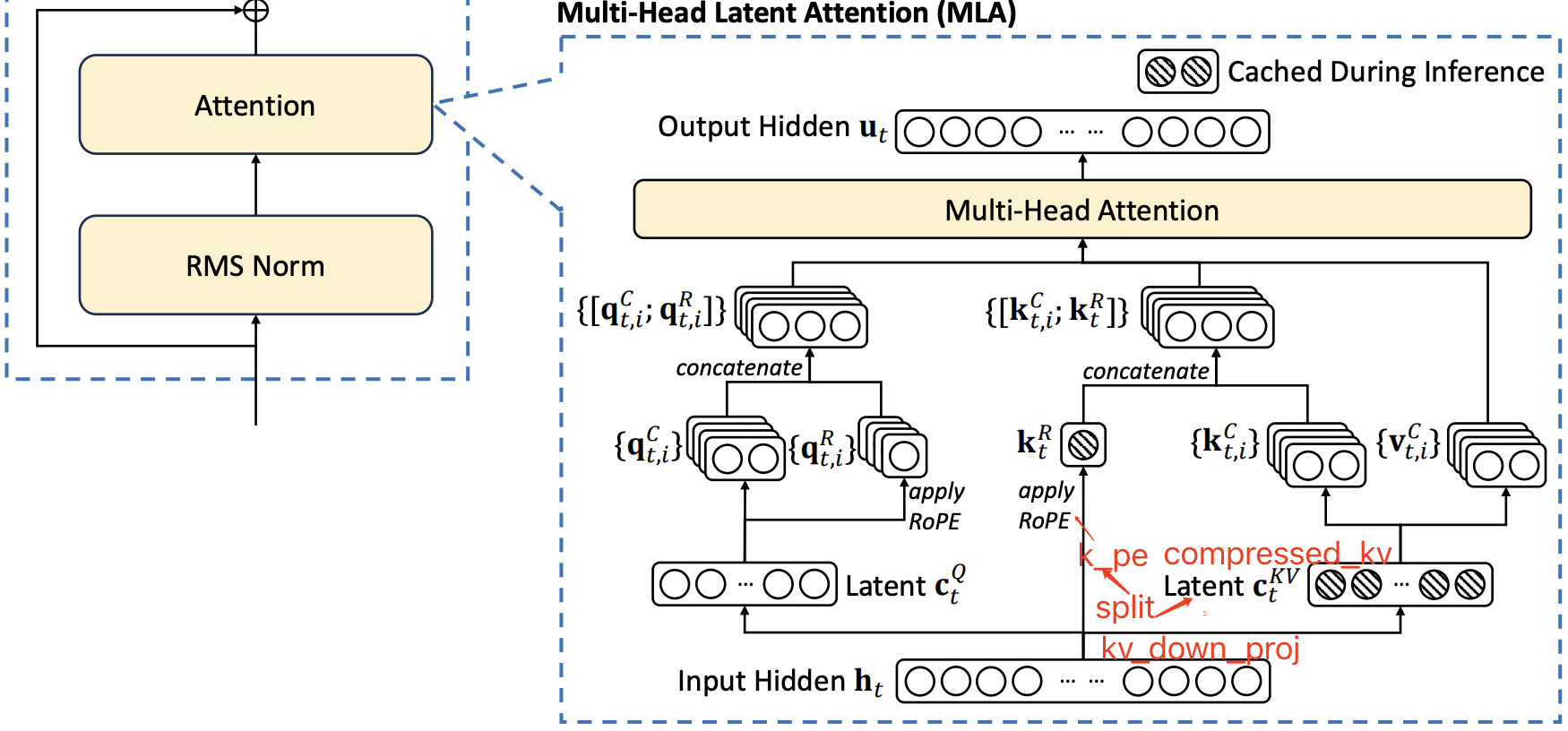
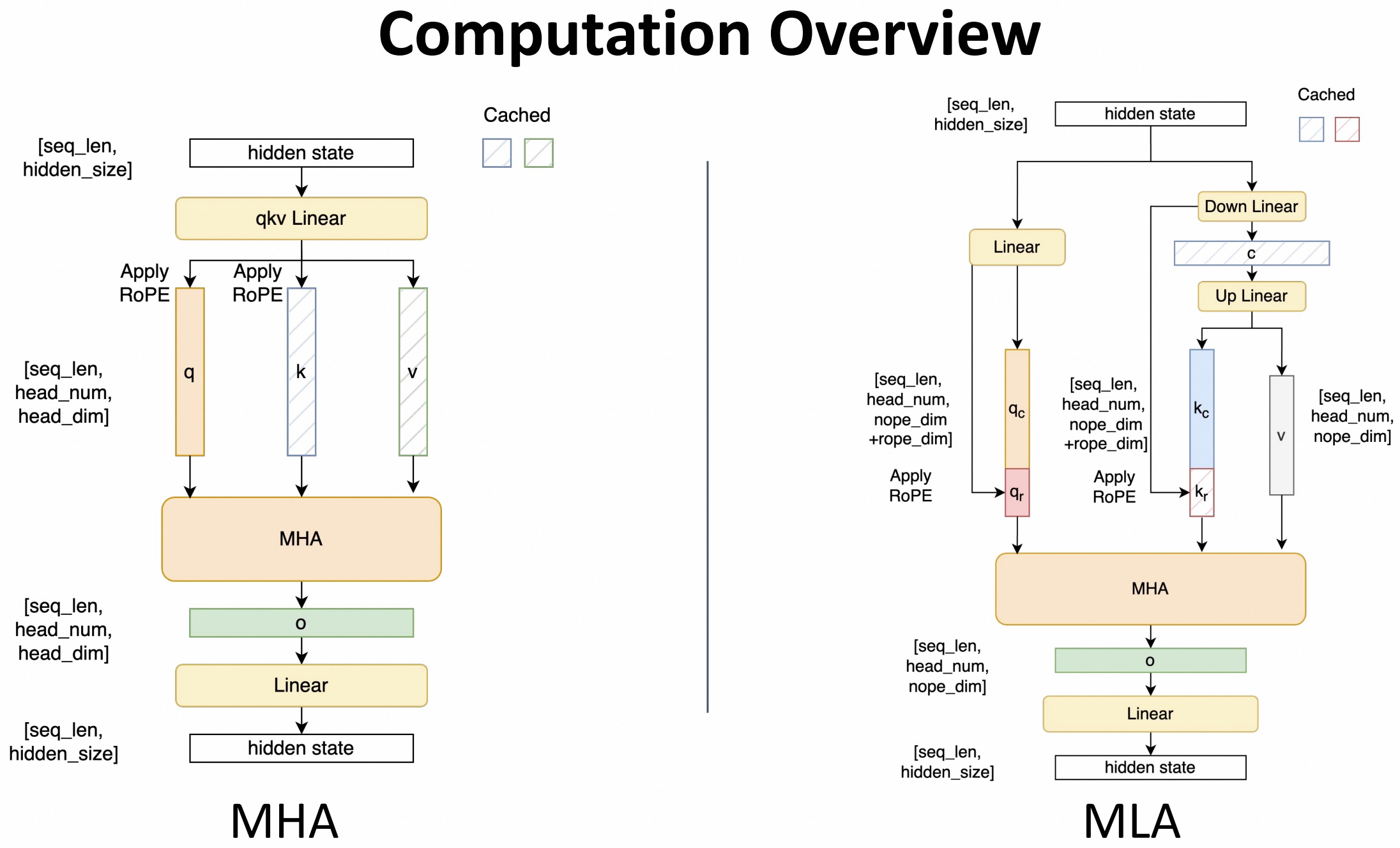
MHA 和 MLA 的结构对比如下所示:
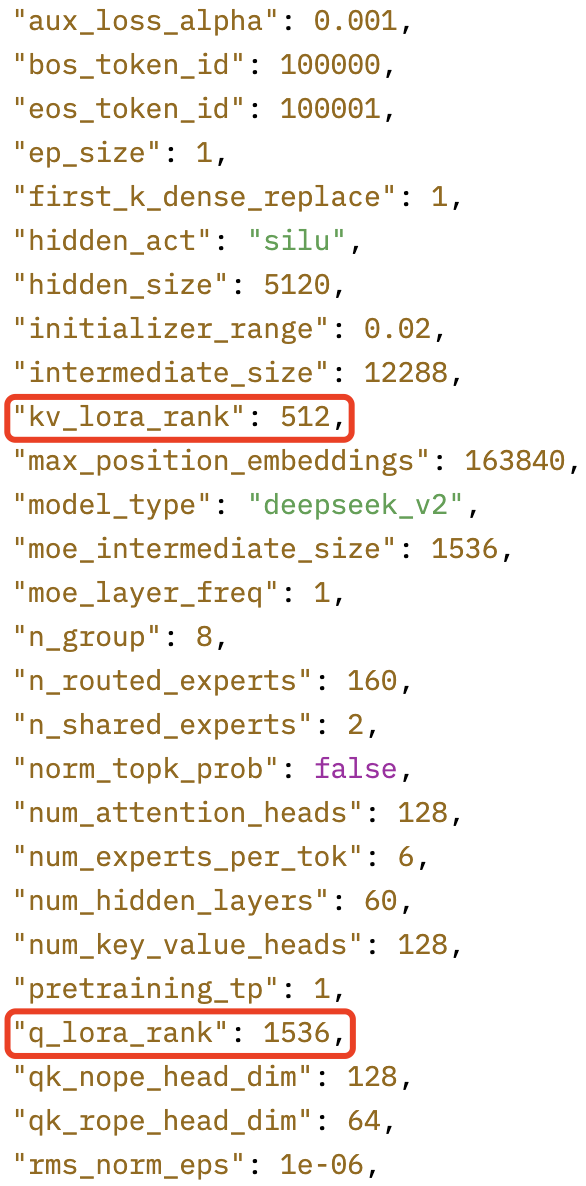
DeepDeekV2 的模型配置如下所示:
1.1 Q 向量计算
大部分参考 DeepSeek-V2高性能推理优化笔记:MLA优化,部分细节做了修改和优化, MLA 结构图以及这章节的公式更多的是给出 MLA 过程和细节,实际的代码实现没有一一对应。
1,在 DeepSeek-V2 中,Q 向量也采用了低秩压缩的方式。首先,将输入向量投影到一个 1536(对应模型配置文件中的 q_lora_rank 参数)维的低维空间,得到 Latent $c_t^Q$。
2,然后,再将其投影到 $\mathbb{R}^{H \times 128}$ 的多头向量空间上(其中 $H=128$ 是 heads 数,对应配置文件中的 qk_nope_head_dim 参数),得到了 Q 向量的第一部分: $q_t^C$。
3,再将其投影到 $\mathbb{R}^{H \times 64}$(对应模型配置文件中的 qk_rope_head_dim 参数)上,并使用 RoPE 嵌入位置信息,得到 Q 向量的第二部分: $q_t^R$。
4,最后,将这两部分进行 concat 拼接得到最终的 $Q$ 向量:$q_t$。
其中:
- $B$:
batch_size批量大小; - $L$:
seq_len序列长度; - $H$:
heads注意力头数; - $\mathbb{R}$ 的最后一维是
head_dim。
1.2 KV 向量计算
1,计算 $KV$ 向量时,首先,将输入向量投影到一个 $512$(对应模型配置文件中的 kv_lora_rank 参数)维的低维空间,得到 Latent $c_t^{KV}$:
2,然后,和 $Q$ 向量的计算过程类似,$K$ 向量的第一部分 $k_t^C$ 是将 $c_t^{KV}$ 通过投影解压缩到 $\mathbb{R}^{H \times 128}$ 的多头向量空间上(其中 $H$ 是 heads 数量,值是 128,$128$ 对应模型配置文件中的 qk_rope_head_dim 参数),计算公式如下:
3,和 Q 向量不同,$K$ 向量的第二部分的 $k_t^R$ 是将输入向量投影到 $\mathbb{R}^{B \times L \times 1 \times 64}$ 单头向量空间($64$ 对应模型配置文件中的 qk_rope_head_dim 参数)维向量空间,并应用 RoPE 嵌入位置信息, 计算公式如下:
4,最后,和 $Q$ 不同,完整的 $K$ 是将 $k_t^R$ 广播到每个 head 后再与 $k_t^C$ concate 拼接得到:
上述广播后拼接的方式意味着,每个 head 的 RoPE 部分是完全相同的。
$V$ 向量因为不需要执行 ROPE 操作,所以它的的计算较为简单,直接将 $c_t^{KV}$ 解压缩(升维)到 $\mathbb{R}^{H \times 128}$ 即可:
注意: $k_t^R$ 和 $c_t^{KV}$ 是需要缓冲的向量。前面计算得到 $q_t$、$k_t$ 和 $\mathbf{v}_t$ 用来执行 self-attention 计算。
1.3 Self-Attention 计算
Self-Attention 的计算过程和传统的 MHA 一模一样。同样也是首先计算 attention score:
\(p = \mathrm{softmax}\left(\frac{q_t^\top k_t + \mathrm{Mask}}{\sqrt{192}}\right) = \mathrm{softmax}\left(\frac{{q_t^C}^\top k_t^C + {q_t^R}^\top k_t^R + \mathrm{Mask}} {\sqrt{128 + 64}} \right) \in \mathbb{R}^{B \times L \times H \times L}\)
计算对 $V$的加权和,并将所有 heads 压平(即 heads * head_dim),得到 Attention 输出:
\[o = p \cdot \mathbf{v}_t \in \mathbb{R}^{B \times L \times H \times 128} \cong \mathbb{R}^{B \times L \times 16384}\]其中,$16384 = 128 \times 128 = \text{num\;attention\;heads * v\;head\;dim}$。最后,经过另一个注意力输出矩阵的投影(5120 是 hidden_size),就能得到 MLA 的最终输出:
2. 标准 MLA 模块的代码实现
transformers 库中的 modeling_deepseek.py 是没有经过推理加速优化的原始实现,我参考其实现给出了一个更为精简和更易看懂的版本,完整代码在这里。
# 从 LlamaAttention 修改而来,适配 DeepseekV2 模型的注意力模块,简单版本不带 kv cache
class DeepseekV2MLA(nn.Module):
def __init__(self, config: DeepseekV2Config):
super().__init__()
# MHA 初始化相关
self.hidden_size = config.hidden_size
self.num_heads = config.num_attention_heads
self.v_head_dim = config.v_head_dim
self.o_proj = nn.Linear(
self.v_head_dim * self.num_heads,
self.hidden_size,
bias=config.attention_bias,
)
self.attention_dropout = config.attention_dropout
self.training = False
self.qk_nope_head_dim = config.qk_nope_head_dim
self.qk_rope_head_dim = config.qk_rope_head_dim
# MLA 相关 part1: 压缩
self.q_lora_rank = config.q_lora_rank
self.kv_lora_rank = config.kv_lora_rank
self.q_down_proj = nn.Linear(self.hidden_size, self.q_lora_rank)
self.q_down_rmsnorm = DeepseekV2RMSNorm(self.q_lora_rank)
self.kv_down_proj = nn.Linear(
self.hidden_size,
self.kv_lora_rank + config.qk_rope_head_dim
)
self.kv_down_rmsnorm = DeepseekV2RMSNorm(self.kv_lora_rank)
# MLA 相关 part2: 解压缩. # W^{WQ} 和 W^{QR} 权重是合并再一起的。
self.qk_head_dim = self.qk_nope_head_dim + self.qk_rope_head_dim
self.q_up_proj = nn.Linear(
self.q_lora_rank,
self.num_heads * self.qk_head_dim,
bias=False,
)
self.kv_up_proj = nn.Linear(
self.kv_lora_rank,
self.num_heads * (self.qk_nope_head_dim + self.v_head_dim),
bias=False,
)
# MLA 相关 part3: 切片 q k 张量,以及 rope 旋转位置编码
self.rotary_emb = DeepseekV2RotaryEmbedding(
config.qk_rope_head_dim,
config.max_position_embeddings,
config.rope_theta,
)
def forward(self, hidden_states, position_ids, casual_mask=None):
batch_size, q_len, hidden_size = hidden_states.shape
# 1,q 压缩和解压缩,以及 split to q_nope, q_rope
q = self.q_up_proj(
self.q_down_rmsnorm(self.q_down_proj(hidden_states))
)
q = q.view(batch_size, q_len, self.num_heads, self.qk_head_dim).transpose(1,2)
q_nope, q_rope = torch.split(
q,
[self.qk_nope_head_dim, self.qk_rope_head_dim],
dim = -1,
)
# 2, kv 压缩和解压缩
kv_down = self.kv_down_proj(hidden_states)
# compressed_kv 压缩后的 kv 张量
compressed_kv, k_rope = torch.split(
kv_down,
[self.kv_lora_rank, self.qk_rope_head_dim],
dim = -1,
)
# num_heads = 1 后续广播其它 heads 上
k_rope = k_rope.view(batch_size, q_len, 1, self.qk_rope_head_dim).transpose(1, 2)
# 对 compressed_kv 解压缩
kv = (
self.kv_up_proj(self.kv_down_rmsnorm(compressed_kv))
.view(batch_size, q_len, self.num_heads, self.qk_nope_head_dim + self.v_head_dim)
.transpose(1, 2)
)
k_nope, value_states = torch.split(
kv,
[self.qk_nope_head_dim, self.v_head_dim],
dim = -1,
)
# 3, 计算 cos 和 sin,并应用 rope 旋转位置编码
kv_seq_len = value_states.shape[-2] # shape (b, nums_head, seq_len, v_head_dim)
cos, sin = self.rotary_emb(value_states, seq_len=kv_seq_len)
q_rope, k_rope = apply_rotary_pos_emb(q_rope, k_rope, cos, sin, position_ids)
# 4, 执行 self-attention 计算
query_states = torch.concat([q_nope, q_rope], dim=-1)
key_states = torch.concat(
[k_nope, k_rope.expand(-1, self.num_heads, -1, -1)],
dim=-1
)
# qk^t
scores = (
torch.matmul(query_states, key_states.transpose(2, 3)) / math.sqrt(self.qk_head_dim)
)
if casual_mask is not None:
scores = scores.masked_fill(casual_mask == 0, float('-inf'))
attn_weights = F.softmax(scores, dim=-1).to(query_states.dtype)
attn_weights = F.dropout(
attn_weights, p=self.attention_dropout, training=self.training
) # attn_weights shape: [bs, num_heads, seq_len, seq_len]
attn_output = torch.matmul(attn_weights, value_states) # shape: [bs, num_heads, seq_len, head_dim]
attn_output = attn_output.transpose(1, 2).contiguous().reshape(batch_size, q_len, self.num_heads * self.v_head_dim)
# 5, MLA 输出映射
output = self.o_proj(attn_output)
return output, attn_weights
标准版 MLA 实现的 forward 推理流程图如下:
graph TD
A[输入隐藏状态 hidden_states] --> B[Query 线性投影]
A --> C[Key-Value 线性投影]
B --> D[Query LoRA 适配]
C --> E[Key-Value LoRA 适配]
D --> F[分离: 基础Q + 旋转Q]
E --> G[分离: 基础K + 旋转K]
E --> H[Value 向量保留]
F --> I[应用旋转位置编码 RoPE]
G --> I
I --> J[合并: 基础Q + 旋转后Q]
I --> K[合并: 基础K + 旋转后K]
J --> L[注意力得分计算]
K --> L
H --> L
L --> M[输出线性投影]
M --> N[输出注意力结果 attn_output]
%% 样式优化
classDef process fill:#e1f5fe,stroke:#01579b,stroke-width:2px;
classDef inputOutput fill:#f3e5f5,stroke:#4a148c,stroke-width:2px;
classDef lora fill:#e8f5e8,stroke:#1b5e20,stroke-width:2px;
classDef rope fill:#fff3e0,stroke:#e65100,stroke-width:2px;
class A,N inputOutput;
class B,C,M process;
class D,E lora;
class I rope;
3 MLA 模块的代码优化-Projection Absorption
3.1 CC (CacheCompressed)
在 transformers 库的 deepseekv3 代码实现中, MLA 算子不缓冲完整的 KV Cache,而是改为缓存压缩后的 KV Cache(即 compressed_kv),与缓存完整的 KV Cache 相比,这将大大减少每个 token 的每层 Cache 大小。
3.2 A_CC(AbsorbCacheCompressed)
DeepSeek-V2 论文中提出,可以将 KV 的解压缩矩阵吸收到 Q-projection 和 Out-projection 中,从而可以在不解压缩 KV Cache的 情况下直接计算最终的 Attention 结果。
1,对于 K 的吸收(吸收进 self-attention 算子中,相当于算子合并),在 Attention Score 的计算公式中,K 向量的非 RoPE 部分的可以做如下展开:
\[{q_t^C}^\top k_t^C = (W^{UQ} c_t^Q)^{\top} W^{UK} c_t^{KV} = {c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK} c_t^{KV} = ({c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK}) c_t^{KV}\]即通过矩阵乘法结合律,可以改为计算 $({c_t^Q}^{\top}{W^{UQ}}^{\top} W^{UK})$,K 的“吸收”核心的优化是 $\text{W}^\text{CombinedK} = ({W^{UQ}}^{\top} W^{UK})$,而这个组合矩阵是可以预先计算出来的。对应的 Attention Score 的计算就简化为:
\[{c_t^Q}^{\top}\ \text{W}^\text{CombinedK}\ c_t^{KV}\]那么做 $K$ 的吸收有什么好处呢?避免重复解压缩出完整的 K 矩阵:在原始版本的解压缩的过程中,由于每个 token 的 key 都需要与 $W^{UK}$ 相乘才能得到 $k_t$ 向量,然后再用 $q_t$ 去点乘这些 $k_t$,这意味着 $W^{UK}$ 要被用到很多次。
总结:A_CC 相比于 CC,把原来属于 kv 的计算量转移到 q 上了,而 q 的 seq_len=1,可减少计算量。其中,$c_t^{KV}$ 是我们实际保存的 KV cache。
2,$V$ 的吸收,其实现更为复杂。为了更方便表述,采用 Einstein 求和约定描述该过程。先定义一些变量:
- b:批大小(batch)
- l:KV 序列长度
- q:Query 序列长度
- h:注意力头数
- c:输入特征维度
- d:每头 Value 维度
- D:最终输出维度
直接生成 Value 向量(基线实现)代码:
# (1) 生成多头 Value:v_t ∈ ℝ^{b×l×h×d}
v_t = einsum('hdc, blc -> blhd', W_UV, c_t_KV)
# (2) 按注意力权重加权求和:o ∈ ℝ^{b×q×h×d}
o = einsum('bqhl, blhd -> bqhd', a, v_t)
# (3) 输出投影:u ∈ ℝ^{b×h×D}
u = einsum('hdD, bhqd -> bhD', W_o, o)
# 将上述三式合并,得到总的计算过程
u = einsum('hdc,blc,bqhl,hdD->bhD', W_UV, c_t_KV, attn_weights, W_o)
结合律优化(延迟投影、避免 v_t)代码:
# (4) 先把注意力权重直接乘到原始上下文,得到 o_ ∈ ℝ^{b×h×q×c}
o_ = einsum('bqhl, blc -> bhqc', attn_weights, c_t_KV)
# (5) 再做 Value 投影:o ∈ ℝ^{b×h×q×d}
o = einsum('bhqc, hdc->bhqd', o_, W_UV) # (5)
# (6) 最终输出:u ∈ ℝ^{b×h×D}
u = einsum('hdD, bhqd -> bhD', W_o, o)
本质上是改变计算顺序的优化: 通过结合律调整计算顺序,减少中间张量的内存占用。
显存对比:
- 基线需要暂存 v_t,大小为 b·l·h·d
- 优化版只产生 o_,大小为 b·h·q·c
- 在长序列(l ≫ q)或 d ≫ c 时能显著降低显存。
计算量对比:
- 基线的矩阵乘法规模:W_UV×c_t_KV ≈ h·d·c × b·l·c → b·l·h·d·c 乘加
- 优化版把乘加推迟到更小的张量
o_上,整体MACs更少。
上述优化方法的实现和对比测试代码如下所示:
import torch
import time
# 配置参数
b, q, l, h, d, c, D = 32, 64, 128, 64, 64, 128, 256 # 将 h 调整为 64
n_warmup = 10 # 预热次数
n_trials = 100 # 正式测试次数
# 初始化张量(GPU)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
W_UV = torch.randn(h, d, c, device=device)
c_t_KV = torch.randn(b, l, c, device=device)
attn_weights = torch.randn(b, q, h, l, device=device)
W_o = torch.randn(h, d, D, device=device) # h 维度为 64
# 预热 GPU
for _ in range(n_warmup):
_ = torch.einsum('hdc,blc->blhd', W_UV, c_t_KV)
_ = torch.einsum('bqhl,blhd->bqhd', attn_weights, _)
_ = torch.einsum('hdD,bhqd->bhD', W_o, _)
# 原始分步实现
def original_method():
v_t = torch.einsum('hdc,blc->blhd', W_UV, c_t_KV)
o = torch.einsum('bqhl,blhd->bqhd', attn_weights, v_t)
u = torch.einsum('hdD,bhqd->bhD', W_o, o.permute(0, 2, 1, 3))
# 优化后实现
def optimized_method():
o_ = torch.einsum('bhql,blc->bhqc', attn_weights.permute(0, 2, 1, 3), c_t_KV)
o = torch.einsum('bhqc,hdc->bhqd', o_, W_UV)
u = torch.einsum('hdD,bhqd->bhD', W_o, o)
# 测量时间
def benchmark(func):
times = []
for _ in range(n_trials):
start = time.time()
func()
end = time.time()
times.append(end - start)
return sum(times) / n_trials
# 执行测试
time_original = benchmark(original_method) * 1000 # 转换为毫秒
time_optimized = benchmark(optimized_method) * 1000
# 打印结果
print(f"原始方法平均时间: {time_original:.3f} ms")
print(f"优化方法平均时间: {time_optimized:.3f} ms")
print(f"速度提升: {time_original / time_optimized - 1:.1%}")
# 验证等价性
def validate_equivalence():
v_t_orig = torch.einsum('hdc,blc->blhd', W_UV, c_t_KV)
o_orig = torch.einsum('bqhl,blhd->bqhd', attn_weights, v_t_orig)
u_orig = torch.einsum('hdD,bhqd->bhD', W_o, o_orig.permute(0, 2, 1, 3))
v_t_opt = torch.einsum('hdc,blc->blhd', W_UV, c_t_KV)
o_opt = torch.einsum('bqhl,blhd->bqhd', attn_weights, v_t_opt)
u_opt = torch.einsum('hdD,bhqd->bhD', W_o, o_opt.permute(0, 2, 1, 3))
# 检查是否等价
assert torch.allclose(u_orig, u_opt, atol=1e-4), "两种方法结果不一致!"
print("两种方法结果一致,验证通过。")
# 调用验证函数
validate_equivalence()
"""
原始方法平均时间: 28.649 ms
优化方法平均时间: 20.378 ms
速度提升: 40.6%
两种方法结果一致,验证通过。
"""